在上一节课中，咱们采取了一种差别于教科书的方法来阐明宇宙学 FLRW 度规的须要性。详细来说，先假设宇宙是静态的，并借助史瓦西解的求解进程，推导出宇宙度规的基础情势，最后将度规推广至静态情况。而本节课斟酌了物资后再推导宇宙度规的情势。3月9日12时，《张向阳的物理课》第二百三十九期开播，搜狐开创人、董事局主席兼CEO、物理学博士张向阳坐镇搜狐视频直播间，在回想总结上一节课内容后，概述了本节课的主题，偏重新梳理了恒星外部解中波及的能动张量、里奇张量跟里奇标量，接着经由过程求解静态宇宙中的爱因斯坦场方程，推导出径向曲率函数的情势及流体的物态方程，终极失掉了宇宙学度规，并进一步阐释了静态宇宙模子的分歧感性。小编： 在上一节课中，咱们采取了一种差别于教科书的方法来阐明宇宙学 FLRW 度规的须要性。详细来说，先假
（张向阳讲授静态宇宙中的流体物态方程）宇宙学度规求解归纳综合在狭义绝对论中研讨宇宙，起首须要明白宇宙的度规情势。这平日依附于宇宙学道理pg电子娱乐平台，即假设宇宙在年夜标准上是平均且各向同性的。基于这一假设，宇宙的度规能够写为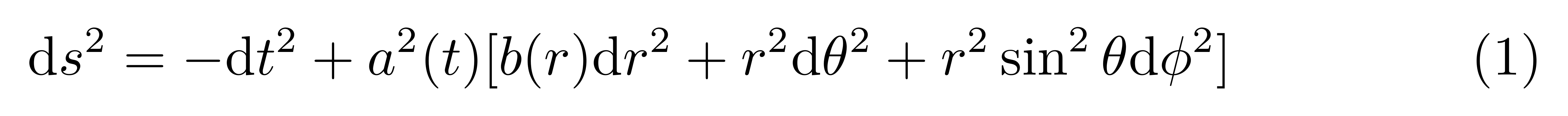 
此中，a(t)是标准因子，描写宇宙收缩或压缩的行动，而b(r)是径向曲率函数，描绘空间的多少何性子。依照狭义绝对论的基础框架，将此度规代入爱因斯坦场方程，可失掉对于a(t)跟b(r)的微分方程，求解后便可失掉宇宙的多少何构造。 开展全文 在静态前提下，咱们能够经由过程以下坐标变更： 
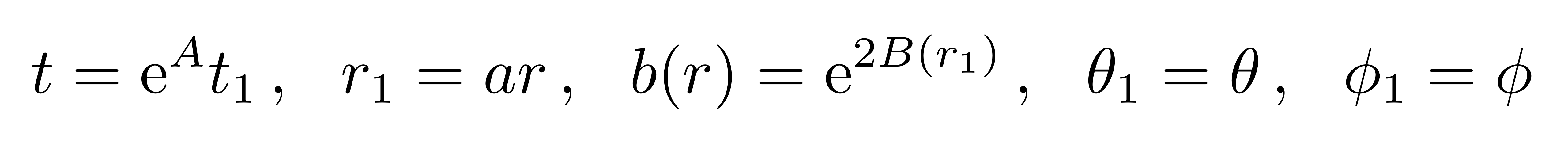将度规变更为熟习的情势 
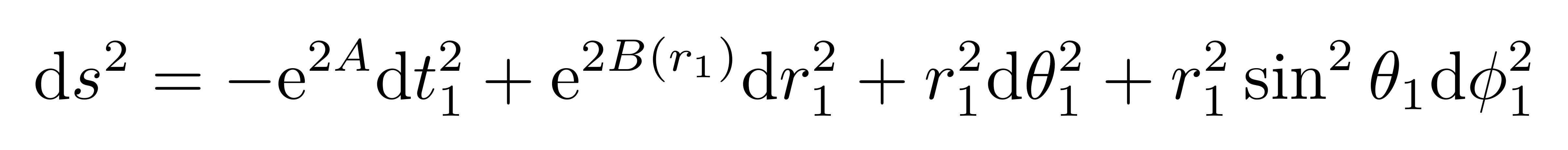此中，A为常数，其导数为零。这恰是求解史瓦西时空时所采取的度规情势，因而咱们能够直接应用先前的史瓦西解推导进程，而无需从新盘算里奇张量跟里奇标量。经由过程爱因斯坦场方程，能够失掉对于B的微分方程。在爱因斯坦场开元捕鱼官方网站方程的右侧，能动张量的情势与恒星外部解相似。咱们曾在求解恒星外部构造时，假设物资满意幻想流体模子，此中包括物资密度跟压强。在恒星外部，球对称性极年夜地简化了成绩，并终极导出了TOV方程。但是，在恒星外部模子中，函数A平日是径向坐标的函数，这使得直接求解A变得极端庞杂，咱们现实上并未直接求解过它。荣幸的是，在宇宙学中，因为平均性假设，A仅为一个常数，从而年夜年夜简化了成绩。在上一节课中，咱们提到宇宙中的物资同样能够看作幻想流体，因而咱们能够直接鉴戒求解恒星外部解的方式，用相似的方法求解B 。终极，经由过程坐标变更，咱们能够回到原始坐标系，并失掉静态前提下度规 (1) 中的径向曲率函数b(r) 。恒星外部解中里奇张量回想在求解史瓦西度规跟恒星外部解时，初始阶段的盘算步调是雷同的：起首由度规盘算里奇张量跟里奇标量，差别仅在于物资的散布差别。史瓦西度规对应的是真空解，而恒星外部解描写的是球对称的幻想流体。对恒星外部解，咱们经由过程爱因斯坦场方程
当前网址：https://www.ajitaro.com//experience/theory/2025/0314/303.html
